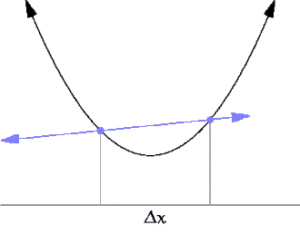
Pour garantir les meilleures expériences, nous utilisons des technologies telles que les cookies pour stocker, ou bien accéder aux informations des appareils. Le fait de consentir à ces technologies nous permettra de traiter des données telles que le comportement de navigation ou les ID uniques sur ce site. Le fait de ne pas consentir ou de retirer son consentement peut avoir un effet négatif sur certaines caractéristiques et fonctions.
La référence à des documents des sites « apprendre la philosophie » et « philo17 », est autorisée par l'autrice de ces sites.
Le stockage ou l’accès technique est strictement nécessaire dans la finalité d’intérêt légitime de permettre l’utilisation d’un service spécifique explicitement demandé par l’abonné ou l’internaute, ou dans le seul but d’effectuer la transmission d’une communication sur un réseau de communications électroniques.
Le stockage ou l’accès technique est nécessaire dans la finalité d’intérêt légitime de stocker des préférences qui ne sont pas demandées par l’abonné ou la personne utilisant le service.
Le stockage ou l’accès technique qui est utilisé exclusivement à des fins statistiques.
Le stockage ou l’accès technique qui est utilisé exclusivement dans des finalités statistiques anonymes. En l’absence d’une assignation à comparaître, d’une conformité volontaire de la part de votre fournisseur d’accès à internet ou d’enregistrements supplémentaires provenant d’une tierce partie, les informations stockées ou extraites à cette seule fin ne peuvent généralement pas être utilisées pour vous identifier.
Le stockage ou l’accès technique est nécessaire pour créer des profils d’internautes afin d’envoyer des publicités, ou pour suivre l’internaute sur un site web ou sur plusieurs sites web ayant des finalités marketing similaires.